Haiti / Élections sénatoriales du 9 août 2015 / Comparaison de la méthode de calcul du CEP et de la méthode de calcul de Montès. (Analyse et Synthèse)

Par Dr. Pierre Montès

Ce travail résume une analyse de la méthode de calcul utilisée par le CEP pour déterminer le pourcentage obtenu par chaque candidat au Sénat. 

On a montré que cette méthode est incorrecte parce qu'elle utilise au dénominateur la somme des voix obtenues par les candidats en lice au lieu d'utiliser la somme des votants, étant donné qu'un votant pouvait voter en donnant 2 voix au maximum (une voix à chacun des deux candidats de son choix). 

On propose la méthode exacte de calcul du pourcentage (Méthode de Montès) dans laquelle le bon dénominateur est introduit (le nombre total de votants ou de bulletins valides dans le département) . 

On compare la méthode de calcul du CEP et la méthode de calcul de Montès. 

On compare également la règle de la majorité absolue utilisée par le CEP et la règle de la majorité absolue proposée dans la méthode de Montès.

On termine  avec un dernier tableau montrant les pourcentages des 4 candidats au Sénat qui arrivent en tête dans chaque département [1].

_____________________________________
[1] Comme le nombre total de votants (ou bulletins de vote valides) n'est pas disponible par département pour les élections sénatoriales, on a approximé cette valeur par le nombre total de votants pour les députés dans le département qui, lui, est disponible. L'électeur (le votant) en entrant au bureau de vote, reçoit deux bulletins en même temps: un pour le choix d'un député, l'autre pour le choix d'un maximum de 2 sénateurs (0, 1 ou 2).On est en droit de faire l'hypothèse de travail selon laquelle l'électeur dépose chacun des bulletins dûment remplis dans leur urne respective. L'erreur commise dans cette approximation est jugée faible, jusqu'à preuve du contraire. La détermination de la vraie valeur du nombre de bulletins de vote pour les deux Sénateurs de chaque département nécessiterait que l'on réanalyse chacun des 13 725 procès-verbaux du vote pour les Sénateurs pour y lire le nombre de votants (bulletins valides) et en faire le total pour chaque département. Pour quelques procès-verbaux que j'ai consultés, l'égalité des deux nombres semble se confirmer, mais il aurait fallu que le CEP fasse vérifier sur un échantillon représentatif des procès-verbaux dans chacun des 10 départements si se confirme cette l'égalité (statistiquement parlant) entre les deux nombres. 
     

1.- L'analogie entre l'opération choix de cours dans une petite école et les élections sénatoriales du 9 août 2015.-

Pour simplifier, on considère une école de 100 étudiants (N=100) où 4 cours différents sont offerts aux étudiants avec la possibilité pour chaque étudiant de choisir un maximum de 2 cours où, dans certaines conditions d'aller plutôt en stage hors de l'école.
Toujours pour simplifier, on considère un département où 100 électeurs (votants) déposent 100 bulletins valides dans l'urne Sénateur (N=100). On considère qu'il y a 4 candidats au Sénat et qu'il faut élire 2 sénateurs. L'électeur peut sur son bulletin de vote voter de l'une des trois manières suivantes pour que son vote soit valide:
1) le votant donne 1 voix à deux des candidats au Sénat en lice en cochant la case sous leur photo;
2) le votant donne 1 voix à un seul candidat au Sénat en cochant la case sous son nom; il ne fait aucun autre choix sur le bulletin;
3)  le votant donne 1 voix à un seul candidat fictif appelé "Aucun candidat" ou "Oken Kandida" (None Of The Above  ou "NOTA" en anglais) en cochant dans la case sous appropriée et il ne fait aucun autre choix sur le bulletin.

L'analogie est la suivante:
a) les 100 étudiants de l'école correspondent aux 100 électeurs du département;
b) les 4 professeurs  de l'école correspondent aux 4 candidats de l'élection sénatoriale dans le département;
c) le stage hors de l'école correspond à NOTA (Aucun candidat) dans l'élection sénatoriale;
d) le formulaire de choix de cours dans l'école correspond au bulletin de vote dans l'élection;
e) la date l'opération choix de cours dans l'école correspond à la date de la tenue du scrutin dans le département.

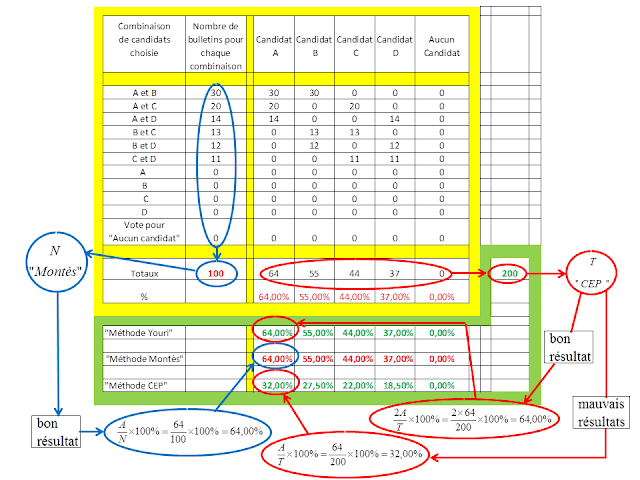
Tableau de l'opération choix de cours et calcul des pourcentages exacts d'étudiants dans chaque cours par rapport au nombre d'élèves dans l'école. Calcul des mêmes pourcentages par la méthode de Montès (méthode exacte) et par la méthode du CEP (erronée).

2.- Tableau des résultats d'une élection fictive dans un département.- 

1) Cas d'un département où N=100, le nombre de candidat au Sénat est 4 et T = 181.

1a) Tableau de calcul pour chaque candidat a) du pourcentage exact du nombre de votants ayant voté pour lui par rapport au nombre total de votants dans le département (méthode de Montès); b) du pourcentage du nombre de voix en sa faveur par rapport au nombre total de voix (méthode du CEP, erronée);  et c) du pourcentage CEP multiplié par 2 (méthode de Youri, incorrecte car T < 2N).

1b) Généralisation et illustration de tous les résultats possibles dans le cas où  il y a 4 candidats au Sénat avec N = 100 bulletins valides  et T = 181 voix valides.

2) Cas d'un département où N=100, le nombre de candidat au Sénat est 4 et T = 200.

2a) Tableau de calcul pour chaque candidat a) du pourcentage exact du nombre de votants ayant voté pour lui par rapport au nombre total de votants dans le département (méthode de Montès); b) du pourcentage du nombre de voix en sa faveur par rapport au nombre total de voix (méthode du CEP, erronée);  et c) du pourcentage CEP multiplié par 2 (méthode de Youri, correcte car T = 2N).

2b) Généralisation et illustration de tous les résultats possibles dans le cas où  il y a 4 candidats au Sénat avec N = 100 bulletins valides  et T = 200 voix valides.

3) Cas d'un département où N=100, le nombre de candidat au Sénat est 4 et T = 200.

3a) Tableau de calcul pour chaque candidat a) du pourcentage exact du nombre de votants ayant voté pour lui par rapport au nombre total de votants dans le département (méthode de Montès); b) du pourcentage du nombre de voix en sa faveur par rapport au nombre total de voix (méthode du CEP, erronée);  et c) du pourcentage CEP multiplié par 2 (méthode de Youri, correcte car T = 2N).

3b) Généralisation et illustration de tous les résultats possibles dans le cas où  il y a 4 candidats au Sénat avec N = 100 bulletins valides  et T = 200 voix valides.

4) Cas d'un département où N=100, le nombre de candidat au Sénat est 4 et T = 133.

4a) Tableau de calcul pour chaque candidat a) du pourcentage exact du nombre de votants ayant voté pour lui par rapport au nombre total de votants dans le département (méthode de Montès); b) du pourcentage du nombre de voix en sa faveur par rapport au nombre total de voix (méthode du CEP, erronée);  et c) du pourcentage CEP multiplié par 2 (méthode de Youri) (incorrecte car T < 2N).

4b) Généralisation et illustration de tous les résultats possibles dans le cas où  il y a 4 candidats au Sénat avec N = 100 bulletins valides  et T = 133 voix valides.

5) Cas d'un département où N=100, le nombre de candidat au Sénat est 4 et T = 200.

5a) Tableau de calcul pour chaque candidat a) du pourcentage exact du nombre de votants ayant voté pour lui par rapport au nombre total de votants dans le département (méthode de Montès); b) du pourcentage du nombre de voix en sa faveur par rapport au nombre total de voix (méthode du CEP, erronée);  et c) du pourcentage CEP multiplié par 2 (méthode de Youri) (correcte car T = 2N).

5b) Généralisation et illustration de tous les résultats possibles dans le cas où  il y a 4 candidats au Sénat avec N = 100 bulletins valides  et T = 200 voix valides.

3.- Comparaison des règles de majorité absolue au premier tour par la méthode de calcul du CEP et la méthode de calcul de Montès .-


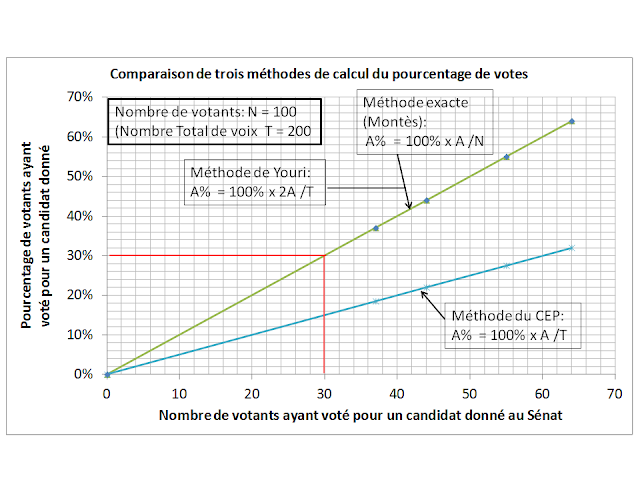
a) On exprime la relation (A/N) = (A/T) * (T/N) sous la forme:

A/T = f (A/N, T/N) = (A/N) / (T/N)

Pour une valeur fixée de A/T (A/T = k1 , k1 pris entre 0 et 100% ), on trace la droite
T/N = (1/k1) * (A/N)

C'est la droite iso-valeur k1 =A/T.

On répète l'opération pour d'autres valeurs k2, ..., kn de A/T.

La figure suivante illustre le résultat obtenu.

Sur cette figure, on illustre la règle de la majorité selon les deux méthodes de calcul: CEP et Montès.
On y voit clairement que la règle de la majorité absolue dans la méthode de Montès est non biaisée, tandis que celle de la méthode du CEP est biasée. Cette dernière rend plus difficile la possibilité pour un candidat d'avoir la majorité absolue.

b) On utilise la relation (A/N) = (A/T) * (T/N) telle quelle:

A/N = f (A/T, T/N) = (A/T)* (T/N)

Pour une valeur fixée de A/N (A/N = p1 , p1 pris entre 0 et 100% ), on trace l'hyperbole

T/N = (p1) / (A/T)

C'est la ligne iso-valeur p1 = A/N.

On répète l'opération pour d'autres valeurs p2, ..., pn de A/N.

La figure suivante illustre le résultat obtenu.

Sur cette figure, on illustre la règle de la majorité selon les deux méthodes de calcul: CEP et Montès.
On y voit clairement que la règle de la majorité absolue dans la méthode du CEP définit implicitement une région assez importante du plan (A/N, T/N) qui soit inaccessible pour candidats au premier tour, quel que soit le résultat qu'il obtient aux élections: pour un T/N donné (pour une élection donnée), le pourcentage maximal (A/T) qu'un candidat puisse atteindre est inférieur à 100% selon la méthode du CEP. Nous l'avions mentionné à plusieurs reprise dans nos analyses antérieures, mais ce graphique montre clairement l'ampleur de ce biais inhérent à la méthode de calcul du CEP.
La méthode de Montès est dépourvue de biais.

c) On utilise la relation (A/N) = (A/T) * (T/N) sous la forme suivante:

A/T = f (A/N, T/N) = (T/N)* (A/N)

Pour une valeur fixée de T/N (T/N = m1 , m1 pris entre 1 et 2), on trace la droite

A/T = (m1) * (A/N)

C'est la droite iso-valeur m1 = T/N.

On répète l'opération pour d'autres valeurs p2, ..., pn de T/N.

La figure suivante illustre le résultat obtenu.

Sur cette figure, on illustre la règle de la majorité selon les deux méthodes de calcul: CEP et Montès.
On y voit clairement que la règle de la majorité absolue dans la méthode du CEP ne permet pas aux candidats dont le couple (A/N, A/T) est situé au 4e quadrant centré au point P d'avoir la majorité absolue alors que la méthode de Montès le permet (région de forme triangulaire CPM. La méthode du CEP réduit donc de manière significative le domaine dans lequel le candidat peut gagner à la majorité absolue.


Les trois figures précédentes qui illustrent à leur manière la même relation entre (A/N), (A/T) et (T/N) ont clairement mis en évidence les défauts de la méthode du CEP et les vertus de la méthode de Montès.

4.- Application de la méthode du CEP et de la méthode de Montès aux données réelles ddu premier tour des sénatoriales de 2015 dans les 10 départements du pays.

    

Ce travail a été fait dans la première analyse produite sur le sujet (24 août 2015).

Pour appliquer la méthode exacte, il aurait fallu connaître le nombre de bulletins valides dans chaque département pour l'élection des sénateurs. Les éléments qui auraient permis de trouver cette donnée sont disponibles dans les procès-verbaux de chaque bureau de vote; mais ces éléments n'ont pas été additionnés pour obtenir le total pour chaque département. Donc cette donnée n'est pas immédiatement disponible au Centre de Tabulation des Voix.

On a donc été amené à faire l'hypothèse que l'électeur qui a déposé un bulletin de vote pour dans l'urne "Député" a aussi déposé au même moment un bulletin de vote dans l'urne "Sénateur" (hypothèse de travail raisonnable). On a donc considéré que le nombre de bulletins comptés  pour les députés dans un département est à peu près égal au nombre de bulletins qu'on aurait comptés pour les sénateurs du même département. (Voir colonne de chiffres en rouge au tableau suivant). On admet que l'erreur commise dans cette approximation soit faible.

Le tableau suivant montre les pourcentages (A/T) et (A/N) obtenus par les 4 candidats au Sénat qui arrivent en tête dans chaque département. Les résultats calculés par la méthode du CEP sous-estiment les vraies valeurs des pourcentages des candidats, tandis ceux calculés par la méthode de Montès, qui auraient dû être exacts, si les bulletins avaient été effectivement comptés, ne devraient pas être aussi éloignés des vraies valeurs des pourcentages comme le sont les résultats du CEP.

Pour les données de l'élections sénatoriales du 9 août 2015 et sous l'hypothèse de travail utilisée, il n'y a pas de candidats au Sénat à avoir un pourcentage supérieur au seuil de 50%  par la méthode de Montès. Cependant le candidat Youri Latortue serait le seul à satisfaire à la règle du 25% d'avance sur son plus proche concurrent.